5.3.1. Transformaciones lineales
Una transformación lineal es una regla que asigna a cada elemento de un conjunto exactamente un elemento de otro conjunto.
Una transformación T de Rn en Rm,que se denota como 
es una regla que asigna a cada vector u Rnun vector único v en Rm.
Rn recibe el nombre de dominio de T y Rm es el codominio. Se representa mediante 
; v es la imagen de u bajo T. El conjunto de imágenes recibe el nombre de rango de T.
Por ejemplo, una transformación 
se puede determinar como
. Donde el dominio de T es R3 y el codominio es R2. Donde la imagen del vector 
se puede determinar estableciendo 
. Entonces la imagen es 
Se dice que una transformación 
es lineal si:
y el vector columna 
. Encuentra la transformación 
de R3 en R2. Usando la transformación encuentra 
.
Haciendo la multiplicación entre matrices:
Por lo tanto, las imágenes son:
Observa que la transformación de una suma de vectores es igual a la suma de sus transformaciones, mientras que la transformación del producto de un vector por un escalar es igual que el escalar por la transformación del vector.
5.3.2 Representación matricial, matrices y transformaciones lineales
En esta sección se verá cómo representar una transformación lineal en espacios vectoriales por medio de una matriz. Así, decimos que una transformación lineal T queda definida si su valor en cada vector del dominio se conoce.
Se representarán los elementos de U y V por medio de vectores de coordenadas, y T por medio de una matriz A que define una transformación de vectores de coordenadas.
Sean U y V espacios vectoriales con bases
una transformación lineal. Si u es un vector en U con imagen T(u) con vectores de coordenadas a y b respecto de estas bases, entonces:
Donde
La matriz A define una transformación de los vectores de coordenadas de U de la misma forma que T transforma los vectores de U.
Ejemplo 1. Considera la transformación lineal 
definida por 
. Encuentra la matriz de T con respecto a las bases 
de R3 y R2, donde:
Utiliza esta matriz para encontrar la imagen del vector 
Se determinan los efectos de T sobre los vectores de la base de R3.
Los vectores de coordenadas 
son 
. Estos vectores forman las columnas de la matriz T.
Se determina el vector de coordenadas u. Usando las combinaciones lineales de vectores:
Se encuentra que 
, siendo el vector de coordenadas u de 
El vector de coordenadas
T(u) es
Por lo tanto, 
Se puede verificar este resultado con la ayuda de la definición 
. En el caso de 
, da
5.3.3 Aplicaciones: Rotación respecto del origen
Considera una rotación 
respecto del origen. Sea:
El paralelogramo 1 se transforma en el paralelogramo 2, puesto que la diagonal del paralelogramo 1 se transforma en la diagonal del paralelogramo 2, como se muestra en la siguiente figura.
Considera una rotación en sentido contrario a las manecillas del reloj en un ángulo 
respecto del origen. Esta rotación transformará el punto A en el punto B, como se muestra en la siguiente figura.
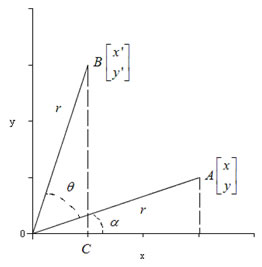
La distancia OA es igual a OB, se denota esta distancia como r. Siendo el ángulo AOC, se tiene que:
Colocando estas expresiones en una sola ecuación matricial:
Por consiguiente:
Una rotación respecto del origen se encuentra definida por una multiplicación entre matrices, confirmando que una rotación es un operador lineal. Si θ es positivo, la rotación es en sentido contrario a las manecillas del reloj; la rotación es a favor de las manecillas del reloj si θ es negativo.
Ejemplo 1. Determina la imagen del punto 
bajo una rotación de 
radianes respecto del origen.
Se obtiene 
en la matriz de rotación:
Observa la gráfica:
