El concepto de "capitalización" es el que estudia y trata de explicar los procesos para trasladar una cifra, un valor, desde el presente hacia el futuro o también desde un futuro próximo a uno más lejano. Este concepto es básico para establecer las fórmulas del monto, de las imposiciones y la determinación de los costos acumulados para ponderar proyectos de inversión.
La operación financiera de descuento es la inversa a la operación de capitalización. Con esta operación se calcula el capital equivalente en un momento anterior de un importe futuro; mientras que la ley de capitalización calcula unos intereses que se les añade al importe principal, compensando el aplazamiento en el tiempo de su disposición. En las leyes de descuento es justo al contrario: se calculan los intereses que hay que pagar por adelantar la disposición del capital.
Capitalización simple
Las operaciones en régimen de simple se caracterizan porque los intereses a medida que se van generando no se acumulan y no generan intereses en periodos siguientes (no son productivos). De esta forma los intereses que se producen en cada periodo se calculan siempre sobre el mismo capital –el inicial –, al tipo de interés vigente en cada periodo.
Este régimen financiero es propio de operaciones a corto plazo (menos de un año).
Se llama capitalización simple a la operación financiera cuyo objeto es la sustitución de un capital presente por otro equivalente con vencimiento posterior, mediante la aplicación de la ley financiera en régimen de simple.
Partiendo de un capital (C0) del que se dispone inicialmente –capital inicial –, se trata de determinar la cuantía final (Cn) que se recuperará en el futuro sabiendo las condiciones en las que la operación se contrata (tiempo – n – y tipo de interés – i –).
Este capital final o montante se irá formando por la acumulación al capital inicial de los intereses que genera la operación periódicamente y que, al no disponerse de ellos hasta el final de la operación, se añaden finalmente al capital inicial.
Los intereses no son productivos, lo que significa que:
- A medida que se generan no se acumulan al capital inicial para producir nuevos intereses en el futuro y, por tanto
- Los intereses de cualquier periodo siempre los genera el capital inicial, al tanto de interés vigente en dicho periodo.
Gráficamente para una operación de tres periodos:

El capital al final de cada periodo es el resultado de añadir al capital existente al inicio del mismo los intereses generados durante dicho periodo. De esta forma, la evolución del montante conseguido en cada momento es el siguiente:
Momento 0: C0
Momento 1: C1 = C0 + I1 = C0 + C0 i = C0 x (1 + i)
Momento 2: C2 = C0 + I1 + I2 = C0 + C0 i + C0 i = C0 x (1 + 2 i)
Momento 3: C3 = C0 + I1 + I2 + I3 = C0 + C0 i + C0 i + C0 i = C0 x (1 + 3 i)
…
Momento n: Cn = C0 + I1 + I2 + … + In = C0 + C0 i + … + C0 i = C0 + C0 x n x i

Expresión aplicable cuando el tipo de interés de la operación se mantiene constante todos los periodos.
A partir de la expresión anterior (denominada fórmula fundamental de la capitalización simple) no solamente se pueden calcular montantes sino que, conocidos tres datos cualesquiera, se podría despejar el cuarto restante.
Finalmente, hay que tener en cuenta que «n» lo que indica es el número de veces que se han generado (y acumulado) intereses al capital inicial; por lo tanto, esa variable siempre ha de estar en la misma unidad de tiempo que el tipo de interés (no importando cuál sea).
Capitalización compuesta
La capitalización compuesta es otra fórmula financiera que también permite calcular el equivalente de un capital en un momento posterior.
La diferencia entre la capitalización simple y la compuesta radica en que en la simple sólo genera intereses el capital inicial, mientras que en la compuesta se considera que los intereses que va generando el capital inicial, ellos mismos van generando nuevos intereses.
Decíamos que la capitalización simple sólo se utiliza en operaciones a corto plazo (menos de un año), mientras que la capitalización compuesta se utiliza tanto en operaciones a corto plazo, como a largo plazo.
En la capitalización compuesta, el capital cambia en cada periodo, pues hay que sumar al capital anterior el interés producido en ese periodo. Designamos con C1 al capital inicial. El segundo capital C2 se obtiene sumando los intereses al primer capital:
C2 = C1 + I1
En el segundo periodo los intereses producidos I2 son mayores por ser mayor el capital C2. Para el tercer periodo el capital es:
C3 = C2 + I2
Y así sucesivamente. Designamos con Ck al capital en el periodo k e Ik el interés producido en ese periodo. Se tiene:
Ck = Ck-1+Ik-1.
Pero como Ik = Ck.i, entonces:
Ck =Ck-1.(1+i)
Si la inversión dura t periodos, los sucesivos capitales se obtienen multiplicando siempre por el mismo número (1+i) y forman una progresión geométrica cuyo primer término es el capital inicial C1 y cuya razón es:
r = (1+i)
El capital final es el término de orden t+1 de la progresión:
F=Ct+1
Utilizando la fórmula para calcular los términos de una progresión geométrica obtenemos:
F=C1.(1+i)t
Tantos equivalentes
Normalmente los tipos de interés suelen venir expresados en términos anuales, pero no siempre se devengan con esa periodicidad, sino que, en la mayoría de las ocasiones, la acumulación de los intereses al capital inicial se hace en periodos más pequeños (meses, trimestres, semestres, etcétera).
La cuestión es, ¿por el hecho de modificar la frecuencia de cálculo de intereses me beneficiaré o, por el contrario, me veré perjudicado? En este sentido, lo lógico es pensar que cualquiera que sea el número de veces que se calculen los intereses, al final el importe total de los mismos no haya variado, esto es, el resultado final de la operación no se vea afectado.
En consecuencia, si se cambia la frecuencia de cálculo de los intereses habrá que cambiar el importe del tanto de interés aplicado en cada caso. Surge el concepto de tantos equivalentes.
Dos tantos cualesquiera, expresados en distintas unidades de tiempo, se dice que son tantos equivalentes cuando aplicados a un mismo capital inicial durante un mismo periodo de tiempo producen el mismo interés o generan el mismo capital final o montante.
¿Cómo se calcula el tipo de interés equivalente, según distinta unidad de tiempo?
La fórmula más sencilla es:

Sobre el cálculo de la tasa equivalente te recomendamos la lectura del documento “Tasa de interés equivalente y curva de rendimientos”, elaborado por el BBVA Bancomer y consultado en agosto 4 de 2008 en: Clic aquí, o bien puedes descargarlo pulsando aquí.
Descuento simple
Se denomina así a la operación financiera que tiene por objeto la sustitución de un capital futuro por otro equivalente con vencimiento presente, mediante la aplicación de la ley financiera de descuento simple. Es una operación inversa a la de capitalización.
Los intereses no son productivos, lo que significa que:
- A medida que se generan no se restan del capital de partida para producir (y restar) nuevos intereses en el futuro y, por tanto,
- Los intereses de cualquier periodo siempre los genera el mismo capital, al tanto de interés vigente en dicho periodo.
En una operación de descuento el punto de partida es un capital futuro conocido (Cn) cuyo vencimiento se quiere adelantar. Deberemos conocer las condiciones en las que se quiere hacer esta anticipación: duración de la operación (tiempo que se anticipa el capital futuro) y tanto de interés aplicado.
El capital que resulte de la operación de descuento (capital actual o presente –C0–) será de cuantía menor, siendo la diferencia entre ambos capitales los intereses que el capital futuro deja de tener por anticipar su vencimiento. En definitiva, si trasladar un capital desde el presente al futuro implica añadirle intereses, hacer la operación inversa, anticipar su vencimiento, supondrá la minoración de esa misma carga financiera.
Gráficamente:

donde:
D: Descuento o rebaja.
Cn: Valor final o nominal.
C0: Valor actual, inicial o efectivo.
i ó d: Tanto de la operación.
Por tanto, el capital presente (C0) es inferior al capital futuro (Cn), y la diferencia entre ambos es lo que se denomina descuento (D). Se cumple la siguiente expresión:
D = Cn – C0
Además, el descuento, propiamente dicho, no es más que una disminución de intereses que experimenta un capital futuro como consecuencia de adelantar su vencimiento; por lo tanto, se calcula como el interés total de un intervalo de tiempo (el que se anticipe el capital futuro). Se cumple:
D = Capital x Tipo x Tiempo
Y, según cual sea el capital que se considere para el cómputo de los intereses, estaremos ante las dos modalidades de descuento que existen en la práctica:
- Descuento racional
- Descuento comercial
En todo caso, y cualquiera que sea la modalidad de descuento que se emplee, en este tipo de operaciones el punto de partida es un capital futuro (Cn) (conocido) que se quiere sustituir por un capital presente (C0) (que habrá de calcular), para lo cual será necesario el ahorro de intereses (descuento) que la operación supone.
1. Descuento comercial
La ley financiera del descuento comercial, que permite calcular el importe del descuento, es la siguiente:
D = Co x d x t
donde:
D son los intereses que hay que pagar
Co es el capital inicial (en el momento t=0)
d es la tasa de descuento que se aplica
t es el tiempo que dura la inversión
Al igual que ya hemos visto con las leyes de capitalización, es importante tener en cuenta que el tipo de interés y el plazo deben referirse a la misma medida temporal.
2. Descuento racional
El ahorro de intereses se calcula sobre el valor efectivo (C0) empleando un tipo de interés efectivo (i).
Al ser C0 (el capital inicial) aquel que genera los intereses en esta operación, igual que ocurría en la capitalización, resulta válida la fórmula de la capitalización simple, siendo ahora la incógnita el capital inicial (C0).
Así pues, a partir de la capitalización simple se despeja el capital inicial, para posteriormente por diferencias determinar el descuento racional:
Cn = C0 (1 + n x i)
• Cálculo del capital inicial:

• Cálculo del ahorro de intereses (Dr):
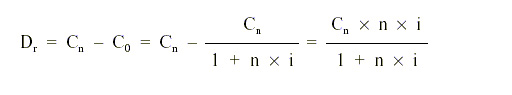
de otra forma

La ley de descuento racional es el equivalente, en sentido inverso, de la ley de capitalización simple, y, al igual que ésta, sólo se suele utilizar en operaciones a menos de un año. Esta relación de equivalencia no se cumple con la ley de descuento comercial.
Con el término equivalente nos referimos al hecho de que descontando un capital a un tipo de interés, y capitalizando el capital resultante con el mismo tipo de interés, volvemos al capital de partida.
Descuento compuesto
La ley financiera de descuento compuesto viene definida de la siguiente manera:
D = Co * (1 - (1 + d) ^ -t)
El signo " ^ " significa "elevado a". Recordemos que "(1+d)^-t" es lo mismo que "1/(1+d)^t"
donde:
D son los intereses de descuento
Co es el capital inicial (en el momento t=0)
d es la tasa de descuento que se aplica
t es el tiempo que dura la inversión
El capital final queda definido de la siguiente manera:
Cf = Co - D
sustituyendo "D"
Cf = Co - ( Co * (1 - (1 + d) ^ -t ))
sacando factor común Co
Cf = Co * (1 - (1 - (1 + d) ^ -t ))
La ley de descuento compuesto es inversa de la ley de capitalización compuesta: si descontamos un capital utilizando el descuento compuesto, y el importe obtenido lo capitalizamos (capitalización compuesta), aplicando el mismo tipo de interés y plazo, obtenemos el importe inicial.
El descuento compuesto, al igual que la capitalización compuesta, se puede utilizar tanto en operaciones de corto plazo (menos de un año), como de medio y largo plazo.
En este sentido contrasta con el descuento comercial y el racional, que sólo se utilizan en operaciones a corto plazo.
Puedes consultar la página web de Abanfin, donde encontrarás una breve y clara explicación sobre el descuento simple y compuesto y una pequeña calculadora en línea para hallarlos. Consultada en agosto 4 de 2008 en: Clic aquí
.